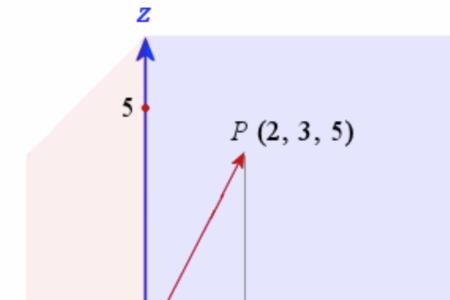
向量的模的计算公式:空间向量模长是²√x²+y²+z²平面向量模长是²√x²+y²。模长是指向量的长度,只有大小数值,没有向量带有的方向性。模是实数,且恒大于等于0。向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。箭头所指的方向表示向量的方向。
向量的模长的运算规则
向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。多个向量的合成用正交分解法,如果要求模一般需要先算出合成后的向量。模是绝对值在二维和三维空间的推广,可以认为就是向量的长度。推广到高维空间中称为范数。
三维向量怎么算模长
三维向量若是知道他的坐标的话,我们可以直接的通过公式计算三维向量的模,若三维向量的坐标为(x,y,z)咋这个三维向量的模为x^2+y^2+z^2等结果,然后再开平方就可以得到三维向量的模,若是知道起点A和终点B的话,可以利用终点坐标减去起点坐标得到向量AB的坐标,然后再利用上述的公式计算
三维向量怎么算模长
1、空间向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:
2、平面向量(x,y),模长是:
扩展资料:
向量的模
1、模只有大小,是个实数,|a|≥0
2、|a|^2=a*a=a^2
3、|a+b|^2=|a|^2+2a*b+|b|^2=a^2+2a*b+b^2
4、||a|-|b||≤|a±b|≤|a|+|b|
5、若a=(x,y),则|a|=√(x^2+y^2)
在线性代数中,向量常采用更为抽象的向量空间(也称为线性空间)来定义。向量是所谓向量空间中的基本构成元素。向量空间是基于物理学或几何学中的空间概念而形成的一个抽象概念,是满足一系列法则的元素的集合,而欧几里得空间便是线性空间的一种。向量空间中的元素就可以被称为向量,而欧几里得向量则是特指欧几里得空间中的向量。