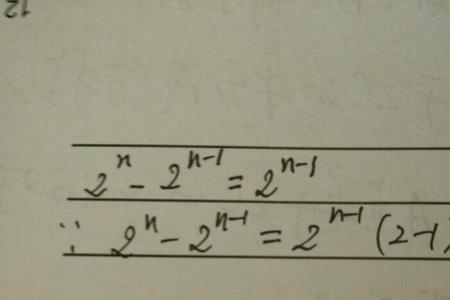数列1/(n^2)求和公式:∑1/(n^2+1),数列(sequence of number),是以正整数集(或它的有限子集)为定义域的函数,是一列有序的数。
数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项,以此类推,排在第n位的数称为这个数列的第n项,通常用an表示。
1/2的n次方求和
(-1)的n次方乘以1/2的n次方
解:
原式=(-1)^n*(1/2)^n
=(-1*1/2)^n
=(-1/2)^n
当n是偶数时,原式=(1/2)^n
当n是奇数时,原式=-(1/2)^n
数列每两项合并为一项
就会发现新的通项公式是4a-1
那么求和就是
2倍a的平方加a
当n为偶数的时候公式为n方/2加上n/2 即n^2/2+n/2
当n为奇数的时候公式为负的偶数时候的 即-n^2/2-n/2
1/2的n次方求和
1/2^n
首先确定为等比数列an=1/2^n
已知an=a1q^(n-1)=(1/2)×(1/2)^(n-1)
即表示为首项为1/2,公比为1/2的等比数列
代入等比数列求和公式:Sn=a1(1-q^n)/(1-q)得:
Sn=(1/2)(1-1/2^n)/(1-1/2)=(1-1/2^n)/(2×1/2)=1-1/2^n
即1/2的n次方和为1-1/2^n