四点共面向量公式

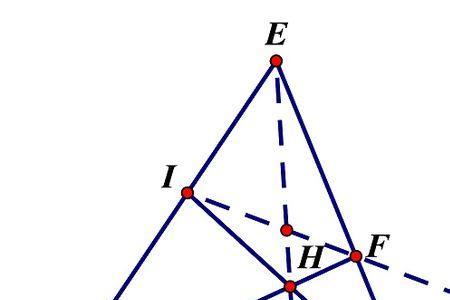
如果通过四点外的一点(空间中)与四点之间的关系来判断折四点共面。A，B，C，D，4个点，与另外一点O，若OA=xOB+yOC+zOD，x+y+z=1，四点就共面3设一向量的坐标为(x，y，z)。

另外一向量的坐标为(a，b，c)。如果(x/a)=(y/b)=(z/c)=常数，则两向量平行如果ax+by+cz=0，则两向量垂直。 三点一定共面，证第四点在该平面内用向量，另取一点O如向量OA=ax向量OB+bx向量OC+cx向量OD，且a+b+c=1则有四点共面。

线平行线：两条线的方向向量矢量积为0，且两条线没交点。面平行线：是线平行面吧，线的方向向量和平面法向量垂直，即线的方向向量和平面法向量数量积为0，且线不在平面内。

四点共面向量公式

一类：纯几何证法。

①要是四个点分别连成两条直线相交了，那必然共面。

②有位置关系，比如两两连成直线以后，出现了这两条直线垂直、平行等现象。

第二类：解析几何证法。假设这四个点是A、B、C、D。（任意两点不重合）

就不说建立空间坐标系的了，就说一下向量方法。

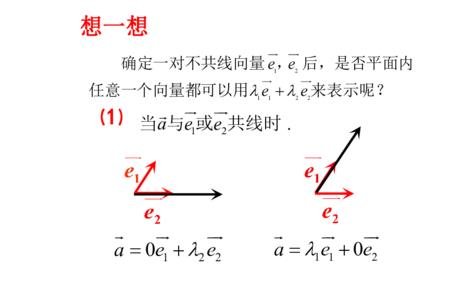
①平面向量基本定理。向量AB、向量AC如果能线性表出AD，也就是存在两个实数α、β使得

α向量AB+β向量AC=向量AD，那么它们就共面。

②先把平面ABC的法向量n找出来，然后用AD点乘n，如果等于0必然D在平面ABC内。