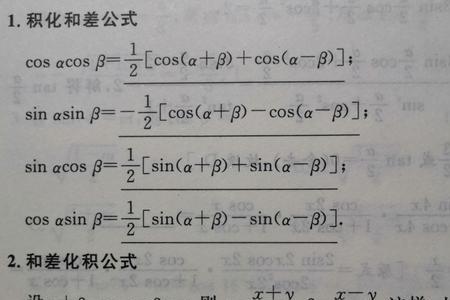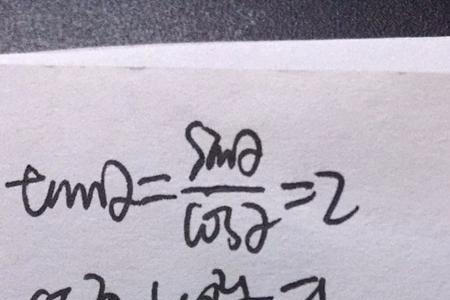tanx-sinx
=sinx/cosx-sinx
=(sinx-sinx*cosx)/cosx
=[sinx(1-cosx)]/cosx
=tanx(1-cosx)
tanx(1-cosx)的等价无穷小为x * x^2 / 2=x^3/2
扩展资料
·积化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化积公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
2022-01-15
30
其他回答5条回答
开心姐姐
tanx-sinx=tanx(1-cosx),x→0时,sinx等价于x,1-cosx等价于1/2×x^2,所以x→0时,tanx-sinx等价于1/2×x^2,是x的3阶无穷小