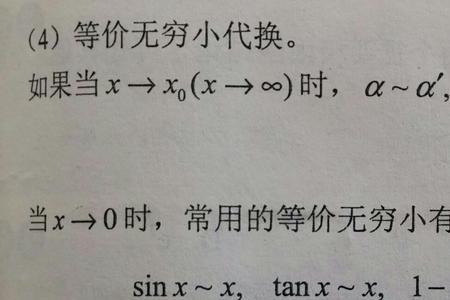为什么sinx和x的等价无穷小

x与sinx是等价无穷小的原因：lim(x→0)sinx/x=1，这就说明x→0时sinx与x是等价无穷小，因此可以代换。

用泰勒公示展开sinx=x-x^3/3！+x^5/5！-x^7/7！+x^9/9！+Rn（x），x趋于0时只剩下x项，其余都是高阶小量，sinx和x等价无穷小，洛必达法则，sinx/x上下分别求导后为cosx/1，x等于0时该值为1，所以sinx和x等价无穷小。

等价无穷小替换

是计算未定型极限的常用方法，它可以使求极限问题化繁为简，化难为易。求极限时，使用等价无穷小的条件：被代换的量，在取极限的时候极限值为0被代换的量，作为被乘或者被除的元素时可以用等价无穷小代换，但是作为加减的元素时就不可以。

为什么sinx和x的等价无穷小

如果lim b/a^n=常数，就说b是a的n阶的无穷小， b和a^n是同阶无穷小。特殊地，如果这个常数是1，且n=1，即lim b/a=1，则称a和b是等价无穷小的关系。

当x趋于0时，sinx/x的极限等于1，这个结论有多种证明方法，根据等价无穷小的概念，我们可以说x趋于0时，sinx和x是等价无穷小。

为什么sinx和x的等价无穷小

当x趋向于0时sinx与x是等价无穷小。说到这个结论我们必须回頋到微分学中一个重要的结论，就是两个重要的极限之一的lim(x→0)sinx/x=|(限于篇幅，这里不证明了)，这个结论在微积分中的应用真不一般。由于这个结论的存在我们就有当x→0时sinx等价于x。