特征根值是什么

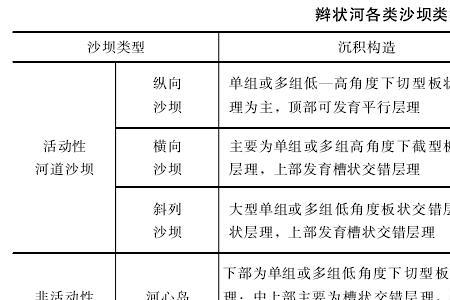
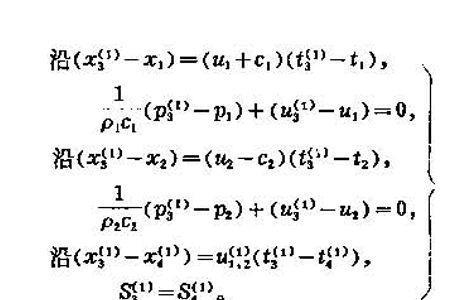特征根是指数学中解常系数线性微分方程的一种通用方法。特征根法也可用于通过数列的递推公式（即差分方程，必须为线性）求通项公式，其本质与微分方程相同。例如 称为二阶齐次线性差分方程： 加权的特征方程。|表对于方阵A，如果存在非零向量x和常数c使得A*x=c*x，那么c叫做A的特征值（特征根）。

多项式|c*I-A|(||表示行列式)的所有根shu恰好是A的所有特征值。

特征根值是什么

特征根值:

设 A 是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是矩阵A的一个特征值（characteristic value)或本征值（eigenvalue)。

非零n维列向量x称为矩阵A的属于（对应于）特征值m的特征向量或本征向量，简称A的特征向量或A的本征向量。

特征根值是什么

特征根是特征方程的根， 单根是只有一个，与其他根都不相同的根， 二重根是有两个根相同。而特征根法是数学中解常系数线性微分方程的一种通用方法。