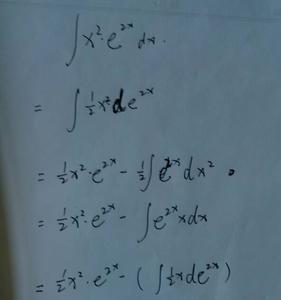x平方除以1-x平方的积分

x的平方除以1-x平方的积分结果及计算过程如下：

令x = tanz，dx = sec²z dz

∫ x²/(x² + 1)² dx

= ∫ (tan²zsec²z)/sec⁴z dz

= ∫ sin²z dz

= (1/2)∫ (1 - cos2z) dz

= (1/2)z - (1/4)sin2z + C

= (1/2)z - (1/2)sinzcosz + C

= (1/2)arctan(x) - (1/2)[x/√zhi(1 + x²)][1/√(1 + x²)] + C

= (1/2)arctan(x) - x/[2(1 + x²)] + C

因为tanz = x/1

所以sinz = x/√(1 + x²)，cosz = 1/√(1 + x²)

扩展资料：

一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。连续函数，一定存在定积分和不定积分。

若在有限区间[a，b]上只有有限个间断点且函数有界，则定积分存在若有跳跃、可去、无穷间断点，则原函数一定不存在，即不定积分一定不存在。

x平方除以1-x平方的积分

即为 (x^2-1+1)/1-x

-（x+1)-1/(x-1)

积分一下即：

-((1/2)x^2+x)-ln(x-1)+C C为常数