e的ln二分之一次幂等二分之一，这是根据对数恆等式得到的。所谓对数恒等式就是α^log(a为底)N=N(a﹥0，a≠1)，本题题目就是α=e时的情况。对数恒等式证明如下：设a^x=N，根据对数定义x=log(a为底)N将它代入a^x=N，就有a^log(a为底)N=N，题目中的e就是a，1/2就是N。
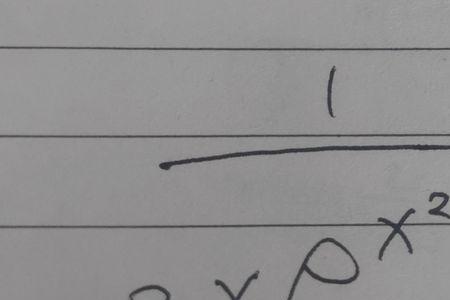
e的ln2分之1次幂等于多少为什么
原创 | 2022-11-30 17:20:55 |浏览：1.6万
猜你想问
-
cycle的动词形式是什么 cyclen. 循环整套系列自行车三轮车周周期工作循环组诗组剧cyclingn. 自行车运动recyclev. 回收利用重新使用使再循环recyclableadj. 能再循环的可回收的recycling... -
herringbone的面料是什么 有以下几种面料：1、牛津纺(Oxford)织物：由于染色和未染色线混纺，产生粗糙感，用它作成的衬衫，既柔软又耐穿。牛津纺织物由许多不同种类，但与细薄平布和府绸衬衫比较，总显... -
deepclone的原理 将对象序列化后写在输出流里，因为写在流里面的对象是一份拷贝，原对象仍然在JVM里然后再把输出流转换为输入流，把对象反序列化后写出来！这样就实现了对象的深度克隆，克... -
attractive的否定形式 unattractive英[ˌʌnəˈtræktɪv]美[ˌʌnəˈtræktɪv]adj. 不吸引人的丑陋的无吸引力的枯燥的[例句]A country that frequently changes government is una... -
comfortable的近义词是什么 近义词是cheerful、cozy、contented，表示舒适的、安适的，例如：1、This restaurant has a cheerful atmosphere.这家餐厅有一种令人愉快的气氛。2、He seemed to like...
