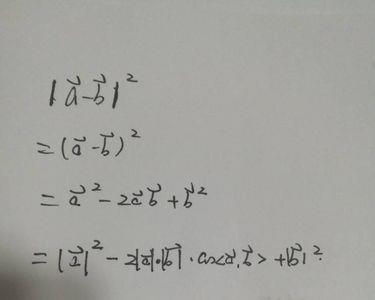
为什么a+b+c等于兀

猜你想问

• 
  为什么梅西中东球迷多 前几年有一个卡塔尔贫民窟的小男孩用一个塑料袋做了一件梅西在阿根廷国家队的10号球衣，染成了蓝白相见的颜色。上还有梅西的名字和号码。梅西知道以后送了这个小男...
• 
  为什么7楼13楼19楼25楼31楼不能买 这只是个人的心理作用，把数字的含义扩大化而已，你所说的楼层，在我这也很受欢迎，反而是，八屋，十四屋及十八屋不太受青睐！买房人都尽量避之，但也都卖出去了，这没什么科学依据...
• 
  网线测线仪g灯为什么不亮 网络g灯不亮 可能原因如下。1、机房光口发光较低或不发光，造成用户端光猫工作不正常，此时光信号灯收不到光缆上发来的光信号或收光信号功率过低，会造成光猫跟机房不...
• 
  为什么把蛋清冻出冰碴再打发 把鸡蛋放到冰箱里冷冻，再拿出来不容易打发。因为冷冻过的鸡蛋蛋清蛋黄已经凝固了，而凝固的地带更不容易打发，为什么不用新鲜的鸡蛋来打发呢新鲜的鸡蛋更容易打成泡沫...
• 
  19楼为什么会有苍蝇 现在的苍蝇蚊子都喜欢往高处飞，似乎不合常理，但每个高楼层的人家都这样，19楼有苍蝇很正常。高层出现蚊子的原因，一是越来越多的人喜欢在自家阳台上种一些植物，养一些小...