把[0,1]区间n等分,则每份为◇Xi=1/n, 则分点Xi=i/n,则小区间长度最大者趋于0即n→∞ 取每个小区间的右端点为§i=Xi=i/n,则f(§i)=e^(i/n) 则和∑(i=1到n)f(§i)◇Xi = 1/n ∑e^(i/n)★ 对★中的和用【等比数列前n项和的公式】 得到★=1/n * e^(1/n)*(1-e) / 1-e^(1/n)★★ 对★★取极限n→∞ 注意用等价无穷小替换可以把e^(1/n) - 1替换成1/n 求得极限=e-1,此即所求的定积分值。
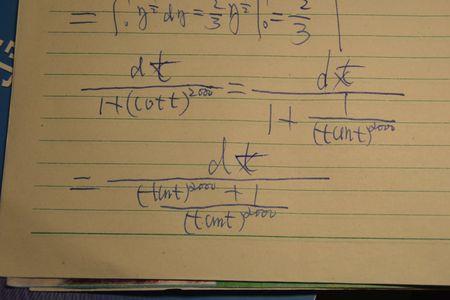
定积分0到1怎么算
原创 | 2022-11-30 14:15:39 |浏览:1.6万
猜你想问
-
 x 的平方乘以cos x 的不定积分 不定积分是x^2sinx-2xcosx+2sinx+c,其中c为任意常数。因为∫x^2cosxdx=∫x^2dsinx=x^2sinx-∫sⅠnxdx^2=x^2sinx-2∫xsinxdx=x^2sinx-2∫xdcosx=x^2sinx-2(xcosx-∫cosx...
x 的平方乘以cos x 的不定积分 不定积分是x^2sinx-2xcosx+2sinx+c,其中c为任意常数。因为∫x^2cosxdx=∫x^2dsinx=x^2sinx-∫sⅠnxdx^2=x^2sinx-2∫xsinxdx=x^2sinx-2∫xdcosx=x^2sinx-2(xcosx-∫cosx... -
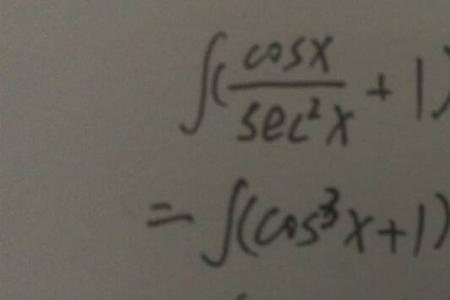 x乘以cosx的不定积分是多少 ∫xcosxdx =∫xdsinx =xsinx-∫sinxdx =xsinx+cosx+C利用牛顿-莱布尼兹公式就可以得到xcosx定积分。连续函数,一定存在定积分和不定积分若在有限区间[a,b]上只有有...
x乘以cosx的不定积分是多少 ∫xcosxdx =∫xdsinx =xsinx-∫sinxdx =xsinx+cosx+C利用牛顿-莱布尼兹公式就可以得到xcosx定积分。连续函数,一定存在定积分和不定积分若在有限区间[a,b]上只有有... -
 卡西欧计算器如何求不定积分 卡西欧计算器求不定积分方法:1、欲计算函数在某点的导数值,首先进入计算页面。2、然后,按SHIFT+3、键输入导数模板。4、在括号里输入函数,在"x="后的框中输入自...
卡西欧计算器如何求不定积分 卡西欧计算器求不定积分方法:1、欲计算函数在某点的导数值,首先进入计算页面。2、然后,按SHIFT+3、键输入导数模板。4、在括号里输入函数,在"x="后的框中输入自... -
 负半轴上的定积分怎么看 函数定积分是在一个区间上积分。无所谓正半轴与负半轴之分,只需要积分区间含于定义域之内。定积分几何意义是由y=f(x),直线X=a(积分下限)x=b(积分上限)及x轴围成曲边四边...
负半轴上的定积分怎么看 函数定积分是在一个区间上积分。无所谓正半轴与负半轴之分,只需要积分区间含于定义域之内。定积分几何意义是由y=f(x),直线X=a(积分下限)x=b(积分上限)及x轴围成曲边四边... -
 cost的3次方的定积分是t的三次方 错了。cost的三次方的不定积分不是t的三次方,而是sint-1/3sin^3t十C。要求cos^3t的不定积分,我们只有用換元法,将被积元索換成sint即可。因为cos^3t=cos^2tcost,从而...
cost的3次方的定积分是t的三次方 错了。cost的三次方的不定积分不是t的三次方,而是sint-1/3sin^3t十C。要求cos^3t的不定积分,我们只有用換元法,将被积元索換成sint即可。因为cos^3t=cos^2tcost,从而...
