双曲螺线公式

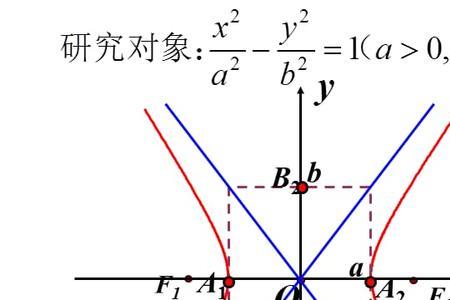
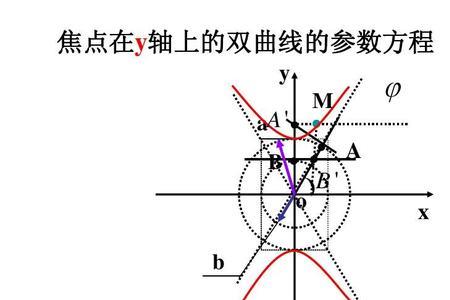
求双曲螺旋线r={acosht，asinht，at}从t＝0起到t＝T的弧长I(T). I(T)=∫{0→T}√[(acosht)'^2+(asinht)'^2+(at)'^2]dt= =a∫{0→T}√[(sinht)^2+(cosht)^2+1]dt= =a∫{0→T}√[2(cosht)^2]dt= =a√2∫{0→T}coshtdt=a√2sinhT.

双曲螺线公式

螺旋函数表达式

在平面极坐标系中，如果极径ρ随极角θ的增加而成比例增加（或减少），这样的动点所形成的轨迹叫做螺线。

最常见的螺线有阿基米德螺线、对数螺线、双曲螺线等。

阿基米德螺线

vertices = 1000

t = from 0 to (20*PI)

a = 0.05

r = a*t

x = r*sin(t)

y = r*cos(t)

双曲螺线公式

双曲螺线(hyperbolic spiral)是指极径和极角成反比例的动点轨迹。双曲螺线的极坐标方程是ρ=a/θ，双曲螺线ρ=a/θ以直线y=a为渐近线，曲线有两支，它们关于Y轴对称。