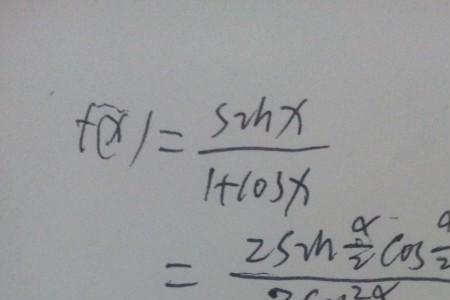2xsinxx的导数
2sinx的导数
2sinx的导数是2cosx。
保留常数2,然后对sinX求导,sinX的导数为cosX,所以2sinX的导数为2cosX。
基本初等函数导数公式主要有以下:
y=f(x)=c (c为常数),则f'(x)=0。
f(x)=x^zhin (n不等于0) f'(x)=nx^(n-1) (x^n表示x的n次方)。
f(x)=sinx f'(x)=cosx。
f(x)=cosx f'(x)=-sinx。
f(x)=a^x f'(x)=a^xlna(a>0且a不等于1,x>0)。
f(x)=e^x f'(x)=e^x。
f(x)=logaX f'(x)=1/xlna (a>0且a不等于1,x>0)。
f(x)=lnx f'(x)=1/x (x>0)。
f(x)=tanx f'(x)=1/cos^2 x。
f(x)=cotx f'(x)=- 1/sin^2 x。
2xsinxx的导数是多少
根据复合函数求导:
(2xsin²x)'=2sin²x+2x×2sinx×cosx
=2sin²x+4xsinxcosx