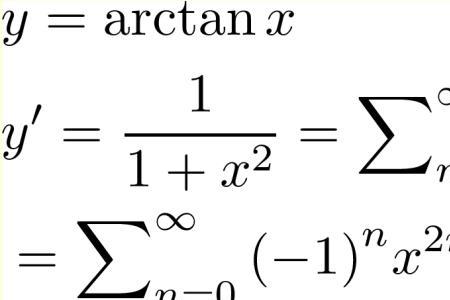常用值有:
arc tan0=0、arc tan(√3/3)=π/6、arc tan1=π/4、arc tan(√3)=π/3、arc tan(-√3/3)=-π/6等。
具体介绍
1、arctan是tan的反函数,就是说知道了tan的函数值,反求这个弧度,他是一个角度,而1/cotx是个函数值,tanx=1/cotx,arctanx不可以理解为tan1/x,看看定义域就知道了,arctan的函数图像与tan关于y=x对称。 arcsin,arccos两个是同一个原理,都是求弧度的,但不完全一样。
2、arctanx(DArctangent)指反正切函数。反函数与原函数关于y=x的对称点的导数互为倒数。设原函数为y=f(x),则其反函数在y点的导数与f'(x)互为倒数(即原函数,前提要f'(x)存在且不为0)。如果函数x=f(y)x=f(y)在区间IyIy内单调、可导且f′(y)≠0f′(y)≠0,那么它的反函数y=f1(x)y=f1(x)在区间Ix={x|x=f(y),y∈Iy}Ix={x|x=f(y),y∈Iy}内也可导。
3、tanx是正切函数,其定义域是{x|x≠(π/2)+kπ,k∈Z},值域是R。arctanx是反正切函数,其定义域是R,反正切函数的值域为(-π/2,π/2)。两者的转换公式为y=tanxx=arctany。
arctanx的值表
arctanx没有最值。
arctanx的定义域是:R(全体实数)。
arctanx
1、定义域:R。
2、值 域:(-π/2,π/2)。
3、奇偶性:奇函数。
4、周期性:不是周期函数。
5、单调性:(-∞,﹢∞)单调递增。
扩展资料:
三角函数最值求法归纳:
1、一角一次一函数形式
即将原函数关系式化为:y=Asin(wx+φ)+b或y=Acos(wx+φ)+b或y=Atan(wx+φ)+b的形式即可利用三角函数基本图像求出最值。
2、一角二次一函数形式
如果函数化不成同一个角的三角函数,那么我们就可以利用三角函数内部的关系进行换元,以简化计算。最常见的是sinx+cosx和sinxcosx以及sinx-cosx之间的换元。