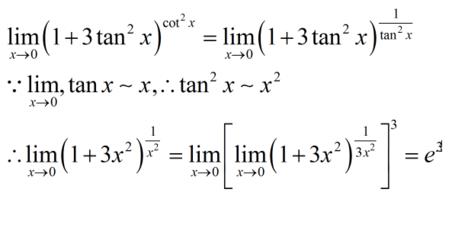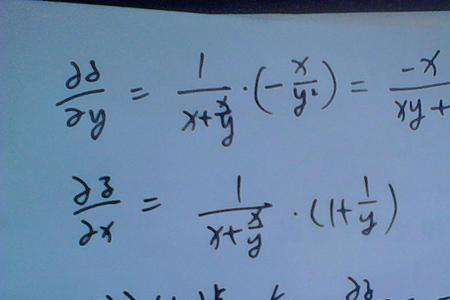左边先对y求导然后y对X再求导(即所谓对X求偏导。从高中层次看可理解为复合函数求导),右边正常对X求导。本题左边求导为y'/y,右边对X求导后为lna,所以y'=ylna。若先化简得y=a^x,求导y'=a^xlna。这与上述两边同时对X求导结果是一致。
lny=xlna两边怎么同时对x求导
先说答案,根据隐函数求导法则和自然对数函数的求导法则来求。
再说完整操作过程,我将它分解为以下二个步骤完成,希望能帮到你:
第一步,因为lny=xlna
两边对x求导得
y’/y=lna
所以y’=ylna。
第二步,求y
因为lny=xlna
所以lny=lna^x
因此y=a^x
因而y’=a^xlna。