两条直线关于点对称公式

b/k-m/k，ka+m）

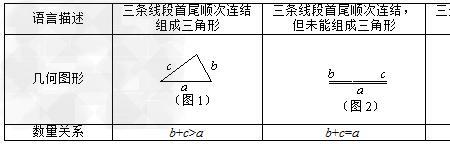
关于直线对称公式如下

1、点（a，b）关于直线 y=kx+m （k=1或-1）的对称点为：（b/k-m/k，ka+m），实际上是将表达式中的x，y的值互换，因为直线方程 y=kx+m 中有 x=y/k-m/k 且 y=kx+m，这种方法只适用于 k=1或-1

的情况.还可以推广为 曲线 f（x，y）=0关于直线 y=kx+m 的 对称曲线 为f（y/k-m/k，kx+m）=0.

2、当k不等于1或-1时，点（a，b）关于直线 Ax+By+C=0 的对称点为（a-（2A*（Aa+Bb+C））/(A*A+B*B)，b-（2B*(Aa+Bb+C））/(A*A+B*B))，同样可以扩展到曲线关于直线对称方面，有 f（x，y）=0

关于直线 Ax+By+C=0 的对称曲线为 f（x-（2A*（Ax+By+C））/(A*A+B*B)，y-（2B*(Ax+By+C））/(A*A+B*B))=0.

点（x，y）关于 点（a，b）对称点是 （2a-x，2b-y）曲线 f（x，y）=0 关于 点（a，b）对称曲线为 f（2a-x，2b-y）=0.

已知点A（x0，y0），方程为y=kx+b，求点B(x1，y1)。因为A、B两点关于直线L1对称，所以A、B连线线段的中点C（x3，y3）在直线L1上。

可列出关系式：y3=kx3+b。所以y1+y0/2=y3，x1+x0/2=x3。可求出x1和y1（x0、y0、k、b已知）。

对称点公式

求点A(x1，y1)关于直线l:ax+by+c=0的对称点B(x2，y2)

1、斜率方面

直线L的斜率为K1=-a/b

那么由AB所构成的直线与L是垂直的关系

所以K2=a/b=y1-y2）/(x1-x2)方程①

2、点线方面

对称点与A的中点必在直线上

所以a(x1+x2)/2+b(y1+y2)/2+c=0方程②

联立上述方程，通过代入法，即可得到

x2=-2b*y1-2c/2a

y2=-2a*x1-2c/2

两条直线关于点对称公式

直线关于点对称的直线方程：已知直线l1关于l2与l3对称，若l1为ax+by+c=0，l2为Ax+By+C=0，l3满足（ax+by+c）/(Ax+By+C)=(2Aa+2bB)/(A²+B²）。

一般的，求与直线ax+by+c=0关于x=a0对称的直线方程，先写成a(x-a0)+by+c+aa0=0的形式，再写成a(a0-x)+by+c+aa0=0形式，化简后即是所求值。

一般的，求与直线ax+by+c=0关于y=b0对称的直线方程，先写成ax+b(y-b0)+c+bb0=0的形式，再写ax+b(b0-y)+c+bb0=0成形式，化简后即是的求值。

求对称图形：

⑴点（x1，y1）关于点(x0，y0)对称的点：（2x0-x1，2y0-y1)。

⑵点（x0，y0）关于直线Ax+By+C=0对称的点。

( x0-2A(Ax0+By0+C)/(A^2+B^2) ，y0-2B(Ax0+By0+C)/(A^2+B^2) )。

⑶直线y=kx+b关于点（x0，y0）对称的直线：y-2y0=k(x-2x0)-b。

⑷直线1关于不平行的直线2对称：定点法、动点法、角平分线法。