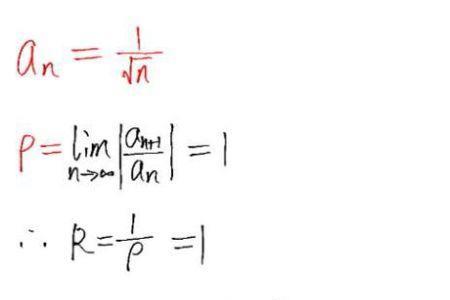an+1/n的收敛半径

基本定理：达朗贝尔审敛法，lim(n∞)|a_(n+1)/a_n|=ρ的时候，∑a_n x^n收敛半径是1/ρ

①∑a_n x^2n，令y=x^2，则该级数等于∑a_n y^n，对y而言收敛半径是1/ρ，也就是|y|<1/ρ时级数收敛，>时发散。

而由于y=x^2，所以|x^2|<1/ρ时级数收敛，>时发散，即：|x|<1/√ρ时收敛，>时发散，所以收敛半径是1/√ρ

②∑a_n (x-2)^n，这个相当于原始级数以2为收敛中心，收敛半径不变

③∑a_n (x-2)^2n，收敛中心是2，收敛半径和∑a_n x^2n相同，是1/√ρ

an+1/n的收敛半径

你的具体问题是什么 已知ρ=lim(n→∞)丨an+1/an丨=0 那么收敛半径R就趋于正无穷 但是首先要确定n趋于无穷大时 通项an是趋于0的，那样的话，这个级数就是收敛的