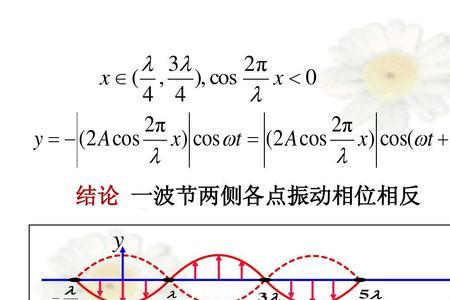
条件:两列传播方向相反、振动方向相同、振幅相同、频率相同。
在波形上,波节和波腹的位置始终是不变的,给人“驻立不动”的印象,但它的瞬时值是随时间而改变的。如果这两种波的幅值相等,则波节的幅值为零。
沿x轴正方向传播的波称为右行波,波动方程为
y1=Acos2π(t/T-x/λ )( 1)
沿x轴负方向传播的波称为左行波,波动方程为
y2=Acos2π(t/T+x/λ ) ( 2)
合成后的驻波方程为式为
y=y1+y2=2Acos2π(x/λ)cos2π(t/T) ( 3)
可见, 合成后的波上的任何一点都在做同一周期的简谐振动。
扩展资料:
对于管中的驻波,当声波传播到闭口端时同样发生反射,入射波和反射波叠加形成驻波。由于弦的固定端和管的闭口端相当于波在传输过程中遇到的障碍物,因此对于波在弦的固定端和管的闭口端发生反射是比较容易接受的。
相邻两波节间的水平距离仍为半个波长,因此驻波的波面包含一系列的波腹和波节,腹节相间,波腹处的波面的高低虽有周期性变化,但此断面的水平位置是固定的,波节的位置也是固定的。
形成驻波的条件公式
一弦线的一端与音叉一臂相连,另一端经支点O并跨过滑轮后与一重物相连。音叉振动后在弦线上产生一自左向右传播的行波,传到支点O后发生反射,弦线中产生一自右向左传播的反射波,当弦长接近1/2波长的整数倍时。两列波叠加后弦线上各点的位移为(设音叉振动规律为u=Acosωt)u(x,t)=2Asin(x)sin(ωt)=A(x)sin(ωt),弦线上每个固定的点均作简谐运动,但不同点的振幅不同,由x值决定。振幅为零的点称为波节,振幅最大处称为波腹。波节两侧的振动相位相反。相邻两波节或波腹间的距离都是半个波长。在行波中能量随波的传播而不断向前传递,其平均能流密度不为零但驻波的平均能流密度等于零,能量只能在波节与波腹间来回运行。
两列振幅相同的相干波在同一直线上沿相反方向传播时互相叠加而成的波,称为驻波。