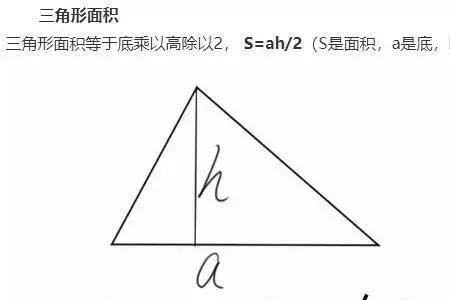
设等边三角形的边长为a,则等边三角形的面积比高等于(1/2)a。
若等边三角形的边长为a,由勾股定理,得等边三角形的高h=(√3/2)a。
由此可知,等边三角形的面积S=(1/2)ah=(1/2)a(√3/2)a=(√3/4)a方。
从而S/h=(√3/4)a方/(√3/2)a=(1/2)a。
等边三角形面积比高等于几比几
答:等边三角形三边相等,三角相等,设边长a,高为h,那么h=√3/2×a,三角形面积S=√3/4×a^2,因此三角形面积比高=S/h=(√3/4a^2)÷(√3/2a)=a/2,也就是说二者之比等于边长一半
等边三角形面积比高等于几比几
等边三角形面积比高等于边长比二。三角形的面积是底乘以高再除以二。等边三角形的面积就等于任意一边除以高再除以二,得到的结果再比高,就等于边长比二。