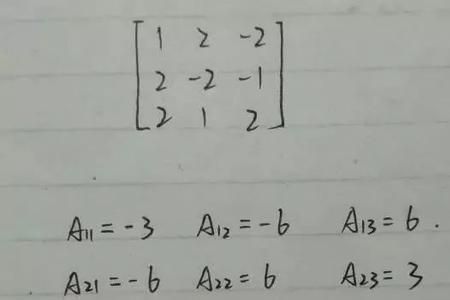例题:
输入矩阵的行列,分别输入两个矩阵,输出矩阵相乘的结果
#include<bits/stdc++.h>
using namespace std
int main(){
int a,b,c
cout<<"请输入两矩阵的行列:"<<endl
cin>>a>>b>>c //分别录入第一个矩阵的行,两矩阵共同行列,第二个矩阵的列
int X[a][b],Y[b][c],Z[a][c] //开辟三个二维数组存储矩阵,注意相乘结果的行列值
cout<<"请输入第一个矩阵:"<<endl
for(int i=0i<ai++){ //矩阵的行
for(int j=0j<bj++){ //矩阵的列
cin>>X[i][j]
}
}
cout<<"请输入第二个矩阵:"<<endl
for(int i=0i<bi++){ //矩阵的行
for(int j=0j<cj++){ //矩阵的列
cin>>Y[i][j]
}
}
memset(Z,0,sizeof(Z)) //将二维数组Z初始化为0
//int temp=0
cout<<"矩阵相乘的结果为:"<<endl
for(int i=0i<ai++){
for(int j=0j<cj++){
for(int k=0k<bk++){
Z[i][j]=Z[i][j]+X[i][k]*Y[k][j] //行与列的乘积和为相应结果值
//temp=temp+X[i][k]*Y[k][j]
}
cout<<Z[i][j]<<" " //计算完一个后输出
//cout<<temp<<" "
//temp=0
}
cout<<endl //计算完一列后输出换行
}
return 0
}
//本程序也可以不开辟存放结果的二维数组矩阵,直接将结果累加到temp中进行输出
//当输出后重新将temp中的值置0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
注意memset函数:
memset函数实现对指定内存空间初始化的作用。
memset(Z,0,sizeof(Z)) //将二维数组Z初始化为0
int float long string sizeof函数返回数组元素空间的4倍数(一元素占4字节)
char sizeof函数返回数组元素空间大小(一元素占1字节)
double sizeof函数返回数组元素空间8倍数(一元素占8字节)
将矩阵相乘的方法体拿出来
#include<bits/stdc++.h>
using namespace std
int jzcheng(int *q, int *w, int h, int l, int k) //定义两个指针,指向二维数组变为一维数组后的首地址
{
int Z[h][k] //h*k
// memset(Z, 0, sizeof(Z)) //将二维数组Z初始化为0
//int temp=0
//cout<<"矩阵相乘的结果为:"<<endl
//cout<<'n'
for(int i = 0 i < h i++)
{
for(int j = 0 j < k j++)
{
Z[i][j]=0
for(int n = 0 n < l n++)
{
Z[i][j] = Z[i][j] + q[i * l + n] * w[n * k + j] //行与列的乘积和为相应结果值,认真思考为什么是这样,看作一维数组
//temp=temp+X[i][k]*Y[k][j]
}
cout << Z[i][j] << " " //计算完一个后输出
//cout<<temp<<" "
//temp=0
}
cout<<'n'
}
}
int main()
{
int a, b, c
cout << "请输入两矩阵的行列:" << endl
cin >> a >> b >> c //分别录入第一个矩阵的行,两矩阵共同行列,第二个矩阵的列
int X[a][b], Y[b][c] //开辟三个二维数组存储矩阵,注意相乘结果的行列值
cout << "请输入第一个矩阵:" << endl
for(int i = 0 i < a i++) //矩阵的行
{
for(int j = 0 j < b j++) //矩阵的列
{
cin >> X[i][j]
}
}
cout << "请输入第二个矩阵:" << endl
for(int i = 0 i < b i++) //矩阵的行
{
for(int j = 0 j < c j++) //矩阵的列
{
cin >> Y[i][j]
}
}
jzcheng(*X, *Y, a, b, c)
//也可写作jzcheng(X[0], Y[0], a, b, c)均代表以a[0][0]为首元素的一维数组可用作指针
return 0
}
//本程序也可以不开辟存放结果的二维数组矩阵,直接将结果累加到temp中进行输出
//当输出后重新将temp中的值置0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
用vector定义二维数组,避免指针情况
#include<bits/stdc++.h>
using namespace std
int jzcheng(vector<vector<int> >X, vector<vector<int> >Y, int h, int l, int k)
{
int Z[h][k]//h*k
memset(Z, 0, sizeof(Z)) //将二维数组Z初始化为0
//int temp=0
cout<<"矩阵相乘的结果为:"<<endl
//cout<<'n'
for(int i = 0 i < h i++)
{
for(int j = 0 j < k j++)
{
//Z[i][j]=0
for(int n = 0 n < l n++)
{
Z[i][j] = Z[i][j] + X[i][n] * Y[n][j] //行与列的乘积和为相应结果值
//temp=temp+X[i][k]*Y[k][j]
}
cout << Z[i][j] << " " //计算完一个后输出
//cout<<temp<<" "
//temp=0
}
cout<<'n'
}
}
int main()
{
int a, b, c
cout << "请输入两矩阵的行列:" << endl
cin >> a >> b >> c //分别录入第一个矩阵的行,两矩阵共同行列,第二个矩阵的列
vector<vector<int> >X
vector<vector<int> >Y
X.resize(a)
for(int i=0i<X.size()i++){
X[i].resize(b)
}
Y.resize(b)
for(int i=0i<Y.size()i++){
Y[i].resize(c)
} //开辟三个二维数组存储矩阵,注意相乘结果的行列值
cout << "请输入第一个矩阵:" << endl
for(int i = 0 i < a i++) //矩阵的行
{
for(int j = 0 j < b j++) //矩阵的列
{
cin >> X[i][j]
}
}
cout << "请输入第二个矩阵:" << endl
for(int i = 0 i < b i++) //矩阵的行
{
for(int j = 0 j < c j++) //矩阵的列
{
cin >> Y[i][j]
}
}
jzcheng(X, Y, a, b, c)
return 0
}
三阶矩阵乘三阶矩阵的例题
给定三阶方阵A:A={{a,b,c},{d,e,f},{p,q,r}},把第一行的第一个数字变成1,也就是用初等矩阵u来左乘A:u = {{1/a, 0, 0}, {0, 1, 0}, {0, 0, 1}}。
让第二行第一个数字变成0:把第三行乘以-d/p,加到第二行上,这个过程对应的初等矩阵是:v=I+(-d/p)*e_(2,3)= {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} + {{0, 0, 0}, {0, 0, -d/p}, {0, 0, 0}}。
再把第一行乘以-p,加到第三行上对应的初等矩阵是:w=I+(-p)*e_(3,1)= {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}} + {{0, 0, 0}, {0, 0, 0}, {-p, 0, 0}}。
再把第三行第二个元素变成0:第二行乘以-(p (-b p + a q))/(a (e p - d q)),加到第三行上,对应的初等矩阵是——x=I+(-(p (-b p + a q))/(a (e p - d q)))*e_(3,2)
={{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}+ {{0, 0, 0}, {0, 0, 0}, {0, -(p (-b p + a q))/(a (e p - d q)), 0}},注意此时的x.(w.(v.(u.A)))是上三角矩阵。
三阶矩阵乘三阶矩阵的例题
三个矩阵相乘时,按照顺序相乘即可,比如ABC,先乘AB,再算ABC,这样是对的也可以先算BC,再算ABC,因为矩阵乘法满足结合律。矩阵乘法的性质:
1、满足乘法结合律: (AB)C=A(BC)2、满足乘法左分配律:(A+B)C=AC+BC 3、满足乘法右分配律:C(A+B)=CA+CB4、满足对数乘的结合性k(AB)=(kA)B=A(kB)
5、转置 (AB)T=BTAT6、矩阵乘法一般不满足交换律乘法结合律:三个数相乘,先把前面两个数相乘,先乘第三个数,或者先把后面两个数相乘,再和第一个数相乘,它们的积不变。字母表示:(a×b)×c=a×(b×c)集合交并集合的交,并运算都满足结合律:交:(A∩B)∩C=A∩(B∩C)并:(A∪B)∪C=A∪(B∪C)矩阵乘法矩阵乘法满足结合律。一个A x B的矩阵乘以一个B x C的矩阵将得到一个A x C的矩阵,时间复杂度为A x B x C。