A经过一系列初等变换等到B,称A与B等价,也就是存在可逆阵PQ使B=PAQ,那么AB秩相等。
而AB相似是存在可逆阵P使B=P-1AP,由此可见相似的结论强于等价。
扩展资料
具有的'性质:
等价一般是指可以通过初等变换变成另一个,本质上只需要两个矩阵秩相同就可以了。是个很宽泛的条件,应用不大。
A相似于B,是存在非异矩阵P,使得PAP^-1=B,这个是线性代数或者高等代数里面最重要的关系,高等代数一半左右都在研究这个。相似可以推出等价。
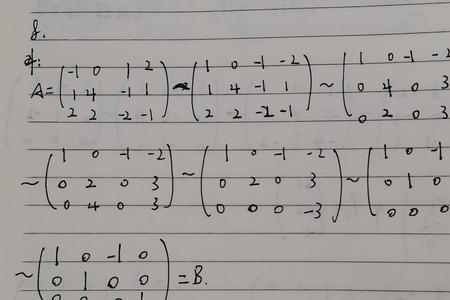
原创 | 2022-11-24 11:23:27 |浏览:1.6万
A经过一系列初等变换等到B,称A与B等价,也就是存在可逆阵PQ使B=PAQ,那么AB秩相等。
而AB相似是存在可逆阵P使B=P-1AP,由此可见相似的结论强于等价。
扩展资料
具有的'性质:
等价一般是指可以通过初等变换变成另一个,本质上只需要两个矩阵秩相同就可以了。是个很宽泛的条件,应用不大。
A相似于B,是存在非异矩阵P,使得PAP^-1=B,这个是线性代数或者高等代数里面最重要的关系,高等代数一半左右都在研究这个。相似可以推出等价。





Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com