结论1:BE DF EF += 证明:延长EB 至G ,使BG =DF 。 先证明ADF ABG ∆≅∆(SAS ), 推导出AG=AF ,∠GAE=∠EAF=45°, 在证明GAE FAE ∆≅∆(SAS ), 即可证明BE DF EF +=。
结论2:EA BEF ∠平分,FA DFE ∠平分 证明:由结论1可知:GAE FAE ∆≅∆, 所以∠GEA=∠FEA , 可证EA BEF ∠平分。 同理可证:FA DFE ∠平分。
结论3:ABE ADF AEF S S S +=△△△
证明:由结论1可知:GAE FAE ∆≅∆,ADF ABG ∆≅∆ 所以ABE ADF AEF S S S +=△△△。
结论4:2CEF C AB =△
证明:由结论1可知:BE DF EF +=, 因为CEF C CE CF EF =++△
所以=2CEF BE C DF CD CB B C A E CF =++=++△
结论5:AH AB =
证明:由结论1可知:GAE FAE ∆≅∆
所以GAE FAE S S ∆∆=, 因为GE EF =, 所以AB AH =。
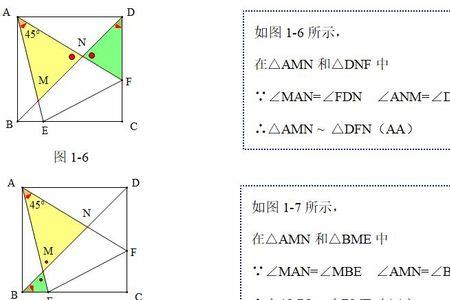
结论6:222BM DN MN +=
证明:如作AQ AN ⊥,=AQ AN ,连接QB QM 、。 先证明ADN ABQ ∆≅∆(SAS ), 推导出=45ABQ ADN ∠∠=︒,QB DN = 在证明QAM NAM ∆≅∆(SAS ), 推到出QM MN =
在QBM Rt △中:222BM QB QM +=,即222BM DN MN +=。