对于函数y=f(x)要证明其单调些有两种方法,第一种定义法:在给定区间或定义域内任取两个自变量ⅹ1,x2,设x1﹤x2,比较f(x1)与f(x2)大小,若f(x1)<f(ⅹ2),则y=f(Ⅹ)单增,若f(x1)>f(x2),则y=f(x)单减。第二种通过求导函数f'(x),若f'(ⅹ)>0,则函数单调递增,若f′(ⅹ)﹤0,则函数单调递减。
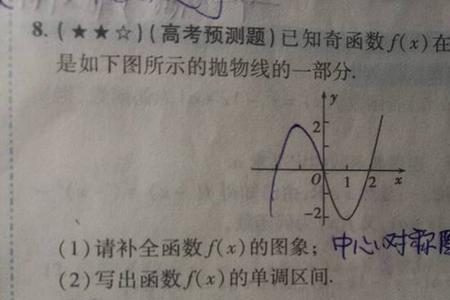
怎样证明是增函数
原创 | 2022-11-22 17:53:08 |浏览:1.6万
猜你想问
-
 南方脚板薯怎样保存 如果量大的话用干沙子,不能用湿的,少的话放通风干燥处,农村常放厨房火塘上面,温度不太高,但干燥是必要的,也可以挖个土洞,把脚板薯放进里面进行储藏!脚扳薯,即脚板薯。因其...
南方脚板薯怎样保存 如果量大的话用干沙子,不能用湿的,少的话放通风干燥处,农村常放厨房火塘上面,温度不太高,但干燥是必要的,也可以挖个土洞,把脚板薯放进里面进行储藏!脚扳薯,即脚板薯。因其... -
 冰丝的防晒效果怎样 冰丝防晒衣是有效果的,最起码穿上凉爽,也可以防晒。防晒衣采用优质的聚酯纤维材质,各种纤维的防晒系数大小:聚酯纤维棉纶人造棉、丝。大多数防晒衣是在布料中加入防晒...
冰丝的防晒效果怎样 冰丝防晒衣是有效果的,最起码穿上凉爽,也可以防晒。防晒衣采用优质的聚酯纤维材质,各种纤维的防晒系数大小:聚酯纤维棉纶人造棉、丝。大多数防晒衣是在布料中加入防晒... -
 在药店卖药这份工作怎样 药店卖药,这份工作怎样如果你是一个女生,在一个在一个大一点的药房工作也是挺不错的,首先,在药店卖药可以学到很多知识,对自己,或者是对家人,对身边的朋友,也是非常有利益...
在药店卖药这份工作怎样 药店卖药,这份工作怎样如果你是一个女生,在一个在一个大一点的药房工作也是挺不错的,首先,在药店卖药可以学到很多知识,对自己,或者是对家人,对身边的朋友,也是非常有利益... -
 用电铲怎样铲墙皮 施工时,建议完全润湿墙壁,可以借助滚筒将墙壁弄湿。之后,电铲通上电,顺着墙皮铲下去就可以快速铲除墙皮。不建议使用化学药品清除墙壁表面,由于腐蚀程度,可能会损坏到墙...
用电铲怎样铲墙皮 施工时,建议完全润湿墙壁,可以借助滚筒将墙壁弄湿。之后,电铲通上电,顺着墙皮铲下去就可以快速铲除墙皮。不建议使用化学药品清除墙壁表面,由于腐蚀程度,可能会损坏到墙... -
 手机号注销了会怎样 这个手机号就不是你本人,与该号码捆绑所有信息会清空,这个最好在注销前,将该号码绑定所有APP解绑或者换绑。然后绑定新的手机号,才行的,而且连银行预留手机号,也要更改...
手机号注销了会怎样 这个手机号就不是你本人,与该号码捆绑所有信息会清空,这个最好在注销前,将该号码绑定所有APP解绑或者换绑。然后绑定新的手机号,才行的,而且连银行预留手机号,也要更改...
