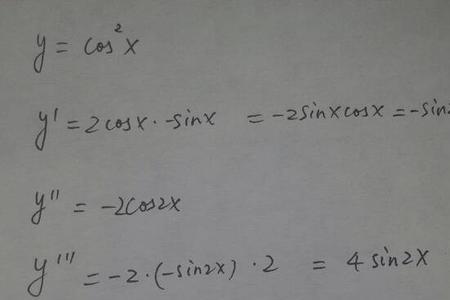y分之一的导数是多少

根据导数公式(x^n)'= nx^(n-1) (n∈Q*)，x分之一是x的-1次方，由此得出x分之一的导数是负的x的平方分之一。

常用导数公式：

C'=0(C为常数函数)

(x^n)'= nx^(n-1) (n∈Q*)

(sinx)' = cosx

(cosx)' = - sinx

(e^x)' = e^x

(a^x)' = （a^x）lna （ln为自然对数）

(Inx)' = 1/x（ln为自然对数）

(logax)' =x^(-1) /lna(a>0且a不等于1)

(x^1/2)'=[2(x^1/2)]^(-1)

(1/x)'=-x^(-2)

y分之一的导数是多少

y分之一求导等于y'=-1*y^(-1-1)=-y^(-2)=-1/y^2。

要注意导数的定义：

1、在某点的领域范围内。

2、趋近于这一点时极限存在，极限存在就要保证左右极限都存在，这一点至关重要。

3、导数定义中一定要出现这一点的函数值， 如果已知告诉等于零，那极限表达式中就可以不出现否就不能推出在这一点可导。

4、掌握导数定义的不同书写形式。

5、前者是对x求导，y是函数不是自变量。后者是对y的求导，y是自变量。

导数的计算

1、基本的求导公式。指数函数、对数函数、幂函数、三角函数和反三角函数这些基本的初等函数数都是需要记住的，这也告诉我们在对函数变形到什么形式的时候就可以直接代公式，也为后面学习不定积分和定积分打基础。

2、常见考试类型的求导。通常在考研中出现四种类型：幂指函数、隐函数、参数方程和抽象函数。这四种类型的求导方法要熟悉，并且可以解决他们之间的综合题，有时候也会与变现积分求导结合。