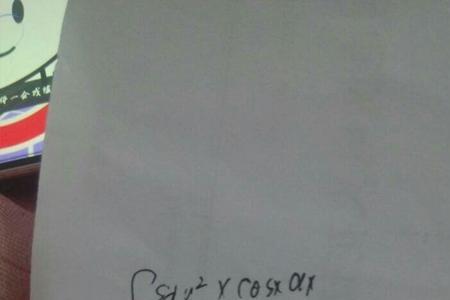e的x分之一的导数是:-e^u/x^2
计算过程如下:
y=(e^(1/x))
设u=1/x
du/dx=-1/x^2
y=(e^u)
dy/dx=dy/du*du/dx=e^u*(-1/x^2)=-e^u/x^2
导函数
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的导函数,记作y'、f'(x)、dy/dx或df(x)/dx,简称导数。