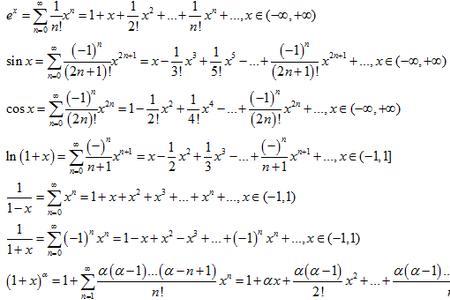不同底数幂的运算法则如下:底数不同,应先化成底数相同再进行计算。
乘法是底数不变,指数相加除法是底数不变,指数相减加法和减法是合并同类项。即同底数幂相乘,底数不变,指数相加同底数幂相除,底数不变,指数相减幂的乘方,底数不变,指数相乘。
不同底数幂的加法公式
(a^m)*(b^m)=(ab)^m 这是积的乘方运算的逆运算。
若底数和指数都不同,则应先转化为底数或指数相同,然后运用法则计算。
若底数不同指数相同,则有(a^m)*(b^m)=(ab)^m这是积的乘方运算的逆运算。
已知中的幂和要求的幂都是2为底,x+1=( x-1)+2,根据同底数幂乘法公式的反向公式“指数相加等于幂相乘”就可以顺利求出最终结果,过程如下:一般的解法是先使用同底数幂乘法公式简化左边的式子,然后根据两个幂相等,如果底相等,那么指数也相等,列方程,最后解方程求出a的值。