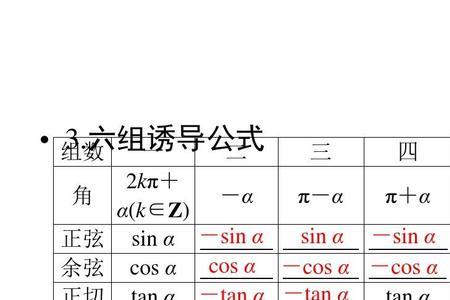
(1)sinx=sin(x+2kπ)
cosx=cos(x+2kπ)
tanx=tan(x+2kπ) k∈Z
原理:终边相同的角同一三角函数值相同(或可用三角函数图像的周期性验证)(2)sin(-x)=-sinx
cos(-x)=cosx
tan(-x)=-tanx
(3)sin(π+x)=-sinx
cos(π+x)=-cosx
tan(π+x)=tanx
(4)sin(π-x)=sinx
cos(π-x)=-cosx
tan(π-x)=-tanx
原理:三角函数值中,正弦一二象限为正,余弦一四象限为正,正切一三象限为正(终边)
(5)sin(π/2+x)=cosx
cos(π/2+x)=-sinx
tan(π/2+x)=-cotx
(6)sin(π/2-x)=cosx
cos(π/2-x)=sinx
tan(π/2-x)=cotx
(7)展开公式
sin(3π/2+x)=sin(π+π/2+x)=-sin(π/2+x)=-cosx
cos(3π/2+x)=cos(π+π/2+x)=-cos(π/2+x)=sinx
tan(3π/2+x)=-cotx
sin(3π/2-x)=sin(π+π/2-x)=-sin(π/2-x)=-cosx
cos(3π/2-x)=cos(π+π/2-x)=-cos(π/2-x)=-sinx
tan(3π/2-x)=cotx