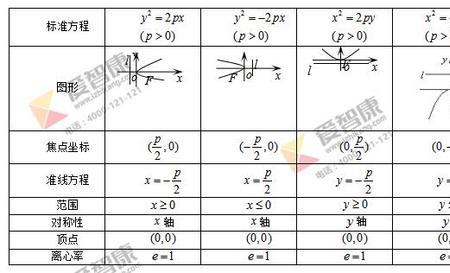
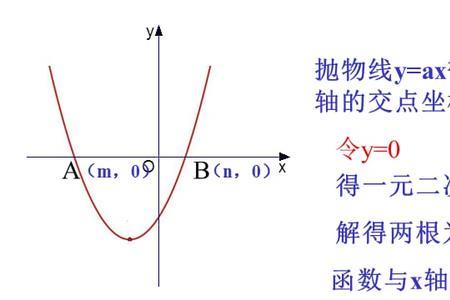
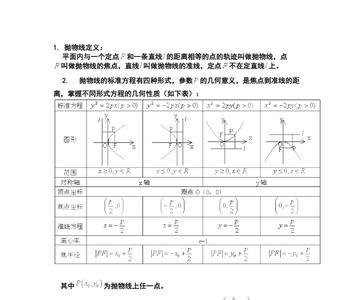
垂直渐近线:就是指当x→C时,y→∞。一般来说,满足分母为0的x的值C,就是所求的渐进线。x = C 就是垂直渐进线。
水平渐近线:就是指在函数f(x)中,x→+∞或-∞时,y→c,y=c就是f(x)的水平渐近线。所以我们需要考虑的是x无限变大或者变小后,y的变化情况。
斜渐近线:这种渐近线的形式为y=kx+b,反映函数在无穷远点的性态,先求k,k=limf(x)/x,再求b,b=limf(x)-kx。极限过程都是x趋向于无穷大
综上所述,我们在算渐近线的时候:
1、 判断其要求的是水平渐近线还是垂直渐近线。
2、 垂直渐近线就是求出使得函数表达式无意义的x取值,即为所求垂直渐近线。
3、 水平渐近线需要简化等式,然后判断随着x的无限变大或变小,y值的变化情况。
扩展资料:
结论:
1、与x^2/a^2-y^2/b^2=1渐近线相同的双曲线的方程,有无数条(且焦点可能在x轴或y轴上)
2、与x^2/a^2-y^2/b^2=1渐近线相同的双曲线可设为x^2/a^2-y^2/b^2=N,进行求解
3、x^2/a^2-y^2/b^2=1的渐近线方程为
b/a*x=y
4、x^2/b^2-y^2/a^2=1的渐近线方程为
a/b*x=y。
求渐近线,可以依据以下结论:
双曲线两渐近线夹角一半的余弦等于a/c且2c为两焦点的距离,2a为轨迹上的点到焦点的距离差。
若极限
存在,且极限lim[f(x)-ax,x→∞]=b也存在,那么曲线y=f(x)具有渐近线y=ax+b。
例:求
渐近线。
解:
(1)x = - 1为其垂直渐近线。
(2)
,即a = 1
,即b = - 1所以y = x - 1也是其渐近线