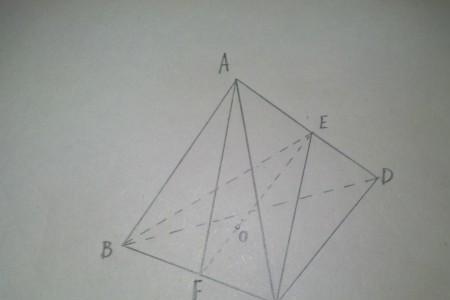
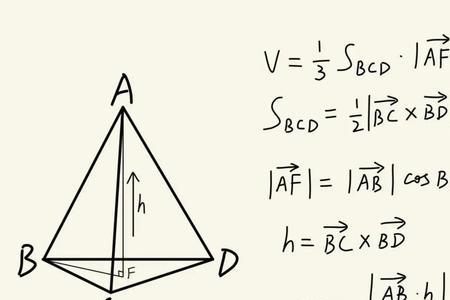设正四面体P-ABC,底面ABC的高为PO,各棱长为a
∵PA=PB=PC
∴OA=OB=OC,(斜线相等,则其射影也相等)
∴O是正△ABC的外心,(重心)
延长OA与BC相交于D
则AD=√3a/2
根据三角形重心的性质
AO=2AD/3=√3a/3
∵△PAO是RT△
∴根据勾股定理
PO^2=PA^2-AO^2
∴PO=√(a^2-a^2/3)= √6a/3
∴正四面体的高为√6a/3.
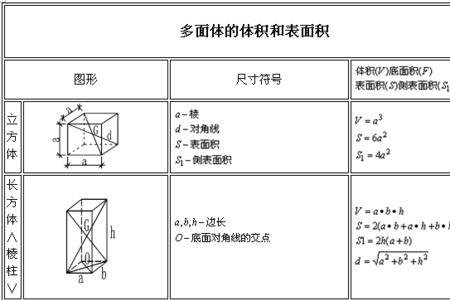
四面体高的公式
作高,高与底面交于底面三角形的垂心,因为正四面体,三线合一,哪个心都一样,在底面作底面三角形的高,算出为根号3/2 L,还是 三线合一,高与地面交点也为重心,长度比2:1,你自己画个正三角形的图就看出来了,2/3 *根号3/2 就是高与一个边组成的三角形的底边