在正态分布的条件下。
中心极限定理,是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量近似服从正态分布的条件。它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。最早的中心极限定理是讨论重点,伯努利试验中,事件A出现的次数渐近于正态分布的问题。
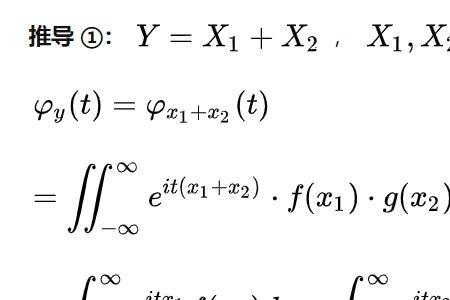
原创 | 2022-11-18 23:31:27 |浏览:1.6万
在正态分布的条件下。
中心极限定理,是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量近似服从正态分布的条件。它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。最早的中心极限定理是讨论重点,伯努利试验中,事件A出现的次数渐近于正态分布的问题。




Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com