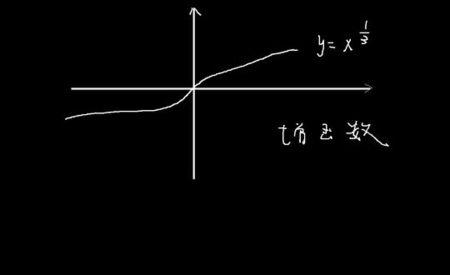
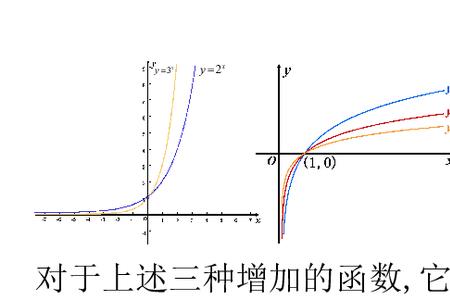
①增函数。设函数f(x)的定义域为D,如果对于定义域D内的某个区间上的任意两个自变量的值x1, x2,当x1<x2时都有f(x1)<f(x2),那么就说f(x)在此区间上是增函数。此区间就叫做函数f(x)的单调增区间。
②减函数。函数f(x)的定义域为I,如果对于定义域I内的某个区间D上的任意两个自变量的值x₁,x₂,当x₁<x₂时,都有f(x₁)>f(x₂),那么就说f(x)在这个区间上是减函数,并称区间D为递减区间。减函数的图像从左往右是下降的,即函数值随自变量的增大而减小。判断一个函数是否为减函数可以通过定义法、图像法、直观法或利用该区间内导数值的正负来判断。
增函数与减函数怎样来区别
增函数与减函数分别代表这个函数是单调递增和单调递减可以通过函数的图像来判断,也可以通过定义来判断。
单调递增函数是指函数值随着x的扩大而单调增加这种函数就是增函数,比如y=x。而单调递减函数是指函数值随着x的增加而减小这种函数叫做减函数,比如说y=-x