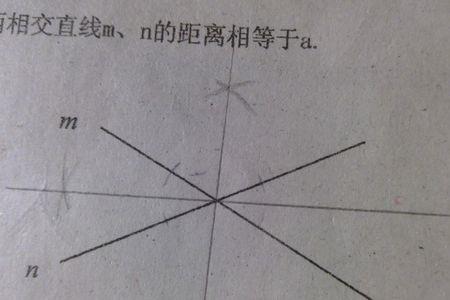
两平行空间直线距离:
L1:(x-x0)/X=(y-y0)/Y=(z-z0)/
L2:(x-x1)/X=(y-y1)/Y=(z-z1)/
令x=x0,y=y0,z=z0得到点M1(x0,y0,z0)
同理得点M2(x1,x2,x3),并做方向向量v=(X,Y,Z)
因为两直线平行,所以两直线间距离d等于点M1到直线L2的距离。
d=|向量v×向量M1M2|/|向量v|
=√(((y0-y1)Z-(z0-z1)Y)+((x0-x1)Y-(y0-y1)X)+((x0-x1)Z-(z0-z1)X))/√(X²+Y²+Z²)