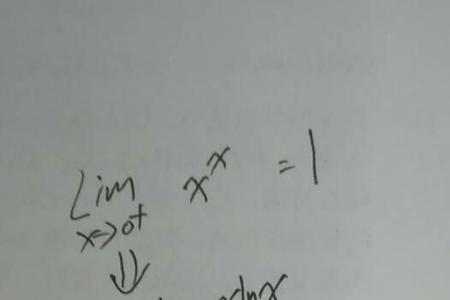e的xy次方整体求导的公式有
一次全导,y'*e^y+xy'+y=0 => y'=-y/(e^y+x)
两边再取全导
y''*e^y+(y')^2*e^y+xy''+y'+y'=0
(e^y+x)*y''+e^y*(y')^2+2y'=0
x=0, y(0)=1, y'(0)=-e^(-1),
e*y''(0)+e*e^(-2)+2[-e^(-1)]=0
ey''(0)=-e^(-1)+2e^(-1)=e^(-1) =1/e
y''(0)=1/e^2
高等数学隐函数求导:
设F(x,y)=y-e^(x*y)=0
由隐函数存在定理得dy/dx=-Fx/Fy
涵义为y对x的导数为负的F(x,y)对x偏导数除以F(x,y)对y的偏导数。
所以求导结果为:y*e^(x*y)/[1-x*e^(x*y)]