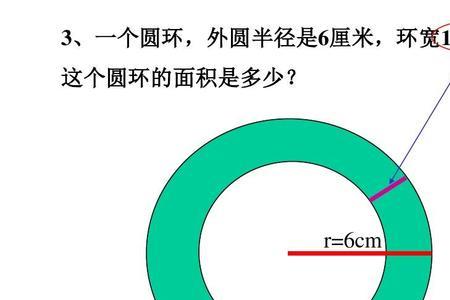
1、S环=π(R²-r²)
环形面积=圆周率乘(大圆半径的平方-小圆半径的平方)
2、S环=π(1/2a)² (a是小圆切线被大圆所截的长度)
环形面积=圆周率乘(小圆切线被大圆截得长度的一半的平方)
3、S环=S(大圆)-S(小圆)=π×r²(大圆)-π×r²(小圆)
还可以写成S环=π(r外²-r内²)解出
4、S环=π(R/2)²(R为小圆的切线)
环形面积=圆周率乘(小圆的切线长度的一半的平方)
扩展资料:
圆的面积计算公式:
或
或
圆的面积求直径:
把圆分成若干等份,可以拼成一个近似的长方形。长方形的宽相当于圆的半径。
圆锥侧面积
(l为母线长)
弧长角度公式
扇形弧长L=圆心角(弧度制)×R= nπR/180(θ为圆心角)(R为扇形半径)
扇形面积S=nπ R²/360=LR/2(L为扇形的弧长)
圆锥底面半径 r=nR/360(r为底面半径)(n为圆心角)
扇形面积公式
R是扇形半径,n是弧所对圆心角度数,π是圆周率,L是扇形对应的弧长。
也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n,如下:
(L为弧长,R为扇形半径)
推导过程:S=πr²×L/2πr=LR/2
(L=│α│·R)
环的面积怎么算
圆环面积求法:
1、圆环面积S=外圆面积-内圆面积=圆周率×(大半径平方-小半径平方)=π(R×R-r×r)=π(R²-r²)。
2、圆环面积S=π[(R-r)×(R+r)]。
R=大圆半径,r=圆环宽度=大圆半径-小圆半径。
圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
生活中的例子有空心钢管,甜甜圈,指环等,截取圆环一部分的叫扇环。
圆的面积 S=πR^2的推导:
1、将圆面一分为二(每一个半圆面包括6个扇形面)
2、将每一个半圆面展开
3、将两个展开的半圆面合拢,围成一个近似长方形(由于分得的扇形较少,得到的是一个近似平行四边形,此时可以通过平移分割思想,将其割补为一个近似长方形)
4、标注这个近似长方形的长为 圆的半周长即:2πr ,高即为圆的半径
5、根据长方形的面积公式 面积=长×宽,可得 S=πr^2。