arccos+arcsin等于多少

arcsinx+arccosx=π/2

设arcsinx=a，arccosx=b

则sina=x，cosb=x=sin(π/2-b)

→sina=sin(π/2-b)→a=π/2-b→a+b=π/2

ARC是数学中的一个基本符号，常写于等号“=”之后，代表等号后的函数为等号前函数的反函数.也常运用于物理运算和几何运算。

扩展资料：

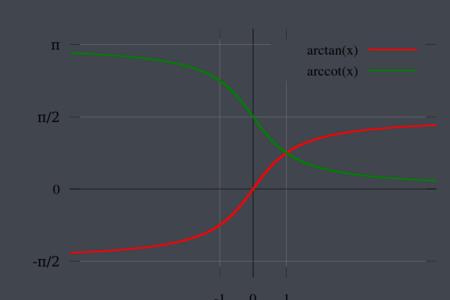
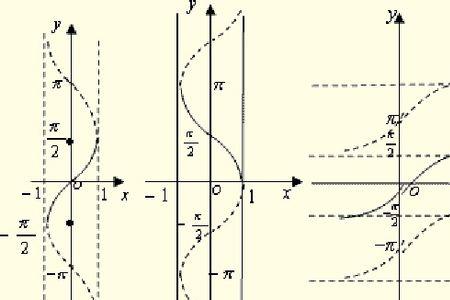
在同一个坐标系中作出函数y=arcsinx和y=arccosx的图象。

设y=arcsinx的图象是曲线AOB，y=arccosx的图象是曲线CMD。显然这两条曲线是关于直线y=π对称的。

在曲线y=arcsinx上任取一点P（x，arcsinx），过P作y轴的平行线，它与直线y=π4的交点是K，与曲线y=arccosx的交点是N（x，arccosx）。

∵|KN|=|KP|

且|KN|=arccosx-π4，|KP|=π4-arcsinx

∴arccosx-π4=π4-arcsinx，也就是arcsinx+arccosx=π2（x∈[-1，1]）。

arccos+arcsin等于多少

arcsin0+arccos0 = 0 + π/2 = π/2 arcsin(x)定义域是[-π/2，π/2] arccos(x)定义域是[0，π]