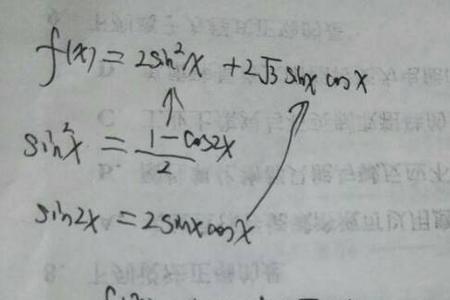1-cos2x=1-(1-2sin2x)=2sin2x。得出方法如下:
因为cos2x=cos²x-sin²x=2cos²x-1=1-2sin²x ,所以1-cos2x=1-(1-2sin2x)=2sin2x。
解析:1-cos2x是与二倍角公式相关的公式变换,因为cos2x=cos²x-sin²x=2cos²x-1=1-2sin²x 属于二倍角公式中的余弦公式。
二倍角公式:
二倍角公式是数学三角函数中常用的一组公式,通过角α的三角函数值的一些变换关系来表示其二倍角2α的三角函数值,二倍角公式包括正弦二倍角公式、余弦二倍角公式以及正切二倍角公式。在计算中可以用来化简计算式、减少求三角函数的次数。
2cos²x
解释:
1 + cos2x = 1 + (cos²x - sin²x)(二倍角公式)
= 1 + (cos²x - 1 + cos²x )
= 1 + (2cos²x-1)
= 2cos²x
扩展内容:
二倍角公式: