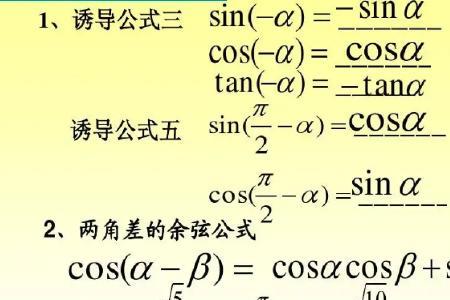arccos和cos之间的转换公式

cos与arccos经过角度和对应的余弦值完成转换。如果cosA＝B，那么arccosB＝A，这里的A是角度，B是数值。cos最终求得的是一个数字，而arccos最终求得的是一个角度。只要知道cos的值，比如cos60°＝1/2，就可以根据这个值来求arccos1/2＝60°＝π/3。可以得出arccos（cos的值）就等于cos的这个角度。cos是余弦函数，arccos其实是反余弦函数，它们关于一三象限的角平分线对称。

arccos和cos之间的转换公式

cos和arccos怎么转换弧长=半径*角度，这里的角度是一个圆弧系统，不是通常的角度系统。既然你知道cos值，那么角度=arccos，只要找到一个反三角函数就可以了。反三角函数可以转换成三角函数。

反三角函数只指三角函数值等于这个数的角度，代表一个角度，而三角函数指的是一个角度的三角函数值。例如：cos60=1/2，arccos 1/2=60。反三角函数是一种基本初等函数。它是反正弦x、反正弦x、反正弦x、反正弦x、反正弦x、反正弦x、反正弦x、反正弦x的总称，分别表示反正弦、反正弦、反余切、反余切的角度为x，为了使单值反三角函数确定的区间具有代表性

往往遵循以下条件：为了保证函数与自变量之间的单值对应，确定的区间必须是单调的函数最好在这个区间内是连续的(这里最好的原因是因为反正切函数和反余切函数是最前沿的)为了方便研究，往往要求所选区间包含0 ~/2的角度确定区间上的函数值域应与整个函数的定义域相同。

这样确定的反三角函数是单值的。为了区别于上面的多值反三角函数，Arc中A的记数法往往改为A，例如单值反正弦函数记为Arcsin X，为了把反三角函数限定为单值函数，把反正弦函数的值Y限定为-/2y/2，把Y看作反正弦函数的主值，写成Y=Arcsin X因此，反余弦函数y=arccos x的主值被限制为0y反正切函数y=反正切x的主值被限制为-/2。