In（1-x）的等价无穷小量是-x。这两个函数，当x→0时，都趋向于0，都是无穷小量。要证明它们是等价的。必须证明，这两函数之比，当x→0时，极限等于1。由罗必达法则，ⅠimⅠn（1-x）／-x=Iim（-1/1-x）／-1=1。所以，已知函数与-x等价无穷小。
ln1-x的等价无穷小推导过程
原创 | 2022-11-17 13:17:21 |浏览：1.6万
猜你想问
-
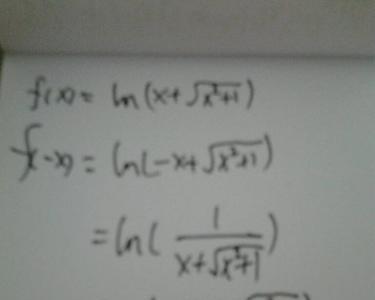lnx等于多少 lnx是对数函数。lnx可以理解为ln(x)，即以e为底x的对数，也就是求e的多少次方等于x。lnx=loge^x。一般地，函数y=logaX（au003e0，且a≠1）叫做对数函数，也就是说以幂（真数）为自... -
lnX=什么 lnx=loge^x。ln是一个算符，它的意思是求自然对数，即以e为底的对数。e是一个常数，约等于2.71828183，lnx可以理解为ln(x)，即以e为底x的对数，所以也就是求e的多少次方等于x... -
y=lnx的公式 y=lnx时，则x=e^y。lnx求导公式推导过程为：由基本的求导公式可以知道y=lnx，那么y'=1/x。如果由定义推导的话，(lnx)'=lim(dx->0) ln(x+dx) -lnx / dx=lim(dx-&g... -
lnx=0怎么算  lnx=0怎么算lnx=0可以这样算x=e^0，就是x=1。对于这种问题，实际上就是考察对数的定义。对于对此的语言算法则应该做的比较熟悉。并能够灵活的应用他们来解决问... -
glng是经度还是纬度 原题中glng似应改写为Greenwich。G.M.T.，或GMT——英文 Greenwich mean time 的缩写符号，意为：格林威治标准时间。地球0度经线标志位于英国格林威治天文台。它是经度...
