在数学空间解析几何中,在三维欧几里德空间的迪卡尔坐标下,两个空间向量a与b可用三维迪卡尔坐标表示,即向量a=(a₁,a₂,a₃)[其中:a₁,a₂,a₃分别是向量a在x,y,z轴上的投影(坐标)]。
向量b=(b₁,b₂,b₃)[其中:b₁,b₂,b₃分别是向量b在x,y,z轴上的投影(坐标)]。
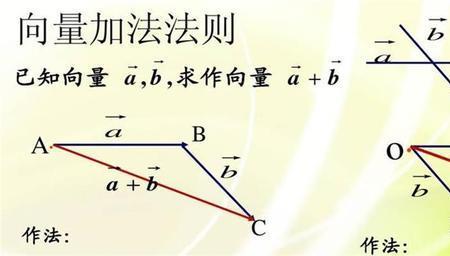
而向量a加向量b就等于(a₁+b₁,a₂+b₂,a₃+b₃)。也就是说两向量相加就是把两向量的坐标相加。
两个向量相加是把坐标相加吗
在x轴上的坐标相加得x轴上的坐标,在y轴上的坐标相加得y轴上的坐标
向量a=(x1,y1),b=(x2,y2),向量a+b=(x1+x2,y1+y2)