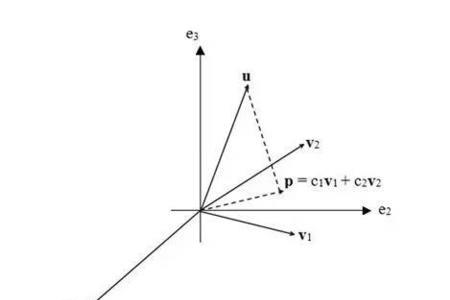
向量的投影具有明显的几何意义,是数量积相关概念的拓展,在实际解决空间向量问题中具有灵活的运用。比如:多个向量在任意轴上的投影和多个或有限个向量的和在任意轴上投影等于各个向量在同一轴上投影的和。
多个向量在任意平面上的投影和多个或有限个向量的和在任意平面上投影等于各个向量在同一平面上投影的和。
原创 | 2022-11-15 19:19:52 |浏览:1.6万
向量的投影具有明显的几何意义,是数量积相关概念的拓展,在实际解决空间向量问题中具有灵活的运用。比如:多个向量在任意轴上的投影和多个或有限个向量的和在任意轴上投影等于各个向量在同一轴上投影的和。
多个向量在任意平面上的投影和多个或有限个向量的和在任意平面上投影等于各个向量在同一平面上投影的和。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com