假设平面向量a的坐标为(x1,y1),向量b的坐标为(x2,y2)。向量a与向量b共线的条件是ⅹ1Y2一x2y1=0。因为两向量共线,那么就存在常数λ,使得向量b=入向量α(入≠0),即(x2,y2)=λ(ⅹ1,y1)=(入x1,入y1),因此根据两个向量相等的条件就有x2=入x1,y2=入y1,消去入就有x1y2=x2y1,即ⅹ1y2一x2y1=0。

平面向量共线的坐标表示的推导
原创 | 2022-11-15 17:20:33 |浏览:1.6万
猜你想问
-
 放大镜平面好还是凸面好 放大镜是凸面的好,才能起到放大作用。因为放大镜本身就是凸透镜。放大镜是利用光的折射原理成像的,本质上来说就是光的折射。为看清楚微小的物体或物体的细节,需要把...
放大镜平面好还是凸面好 放大镜是凸面的好,才能起到放大作用。因为放大镜本身就是凸透镜。放大镜是利用光的折射原理成像的,本质上来说就是光的折射。为看清楚微小的物体或物体的细节,需要把... -
 黄海水平面高程是什么意思 黄海高程是以青岛验潮站1950—1956年验潮资料算得的平均海面为零的高程系统。原点设在青岛市观象山。该原点以“1956年黄海高程系”计算的高程为72.289米。所谓海...
黄海水平面高程是什么意思 黄海高程是以青岛验潮站1950—1956年验潮资料算得的平均海面为零的高程系统。原点设在青岛市观象山。该原点以“1956年黄海高程系”计算的高程为72.289米。所谓海... -
 平面巢适合什么蚂蚁 平面巢一般用于养猛蚁,养攀爬能力不足的蚂蚁,即模仿猛蚁住所,由可以兼顾介质保湿 但应当注意,平面槽(石膏槽)还应当专门安置喂水器,可以是简陋的瓶盖或者水塔都行 造景...
平面巢适合什么蚂蚁 平面巢一般用于养猛蚁,养攀爬能力不足的蚂蚁,即模仿猛蚁住所,由可以兼顾介质保湿 但应当注意,平面槽(石膏槽)还应当专门安置喂水器,可以是简陋的瓶盖或者水塔都行 造景... -
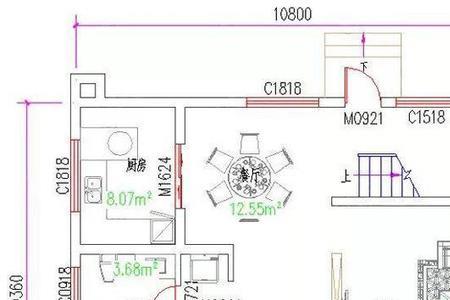 建筑平面开间进深尺寸 住宅设计中,开间是指相邻两个横墙的定位轴线间的距离,因为是就一自然间的宽度而言,所以叫开间,住宅的开间一般不超过3米至3.9米。进深是指一间独立的房屋或一幢住宅建...
建筑平面开间进深尺寸 住宅设计中,开间是指相邻两个横墙的定位轴线间的距离,因为是就一自然间的宽度而言,所以叫开间,住宅的开间一般不超过3米至3.9米。进深是指一间独立的房屋或一幢住宅建... -
 平面铜板高温弯曲是什么原因 这种情况我也经常遇到,一般说来,铜板越薄,被蚀刻的那一面越是容易翘曲,具体原因应该是板材正反两面的应力发生了变化,导致被蚀刻面向上弯曲。解决方法如下充分释放内应...
平面铜板高温弯曲是什么原因 这种情况我也经常遇到,一般说来,铜板越薄,被蚀刻的那一面越是容易翘曲,具体原因应该是板材正反两面的应力发生了变化,导致被蚀刻面向上弯曲。解决方法如下充分释放内应...
