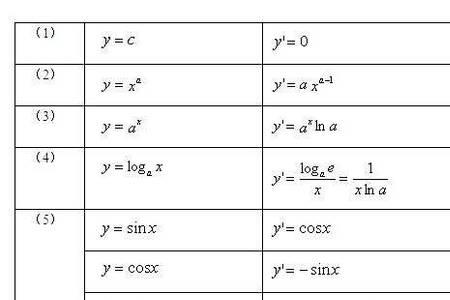logaX的导数是什么

logax的导数：1/(x*lna)。对于可导的函数f(x)，x↦f'(x)也是一个函数，称作f(x)的导函数（简称导数）。

y=logax的导数

由复合函数求导法则

y'=1/(x*lna)

a^y=x

两边对x求导：

y'*lna*a^y=1

y'=1/(a^y*lna)=1/(x*lna)

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续不连续的函数一定不可导。

logaX的导数是什么

以a为底的X的对数 的导数是1/xlna ，以e为底的是1/x

logax=lnx/lna

∫logaxdx=∫lnx/lnadx=1/lna*∫lnxdx

设lnx=t，则x=e^t

∫lnxdx=∫tde^t=te^t-∫e^tdt=te^t-e^t=xlnx-x

所以∫logaxdx=1/lna*∫lnxdx=（xlnx-x）/lna

扩展资料

不定积分的公式

1、∫ a dx = ax + C，a和C都是常数

2、∫ x^a dx = [x^(a + 1)]/(a + 1) + C，其中a为常数且 a ≠ -1

3、∫ 1/x dx = ln|x| + C

4、∫ a^x dx = (1/lna)a^x + C，其中a > 0 且 a ≠ 1

5、∫ e^x dx = e^x + C

6、∫ cosx dx = sinx + C

7、∫ sinx dx = - cosx + C

logaX的导数是什么

f(x)=logax=lnx/lna 相差比例系数1/lna所lnx与导数相差比例系数1/lna即(lnx)'=1/x(logax)'=1/(xlna)