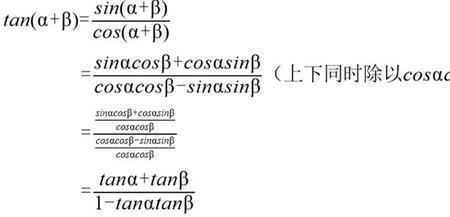三角函数映射法则

一、映射

设X，Y是两个非空集合，如果存在一个法则f

·使得对x中每个元素x 按法则f

·在Y中有唯一确定的元素y与之对应

·则称f为从X到Y的映射 记作f:X->Y

·元素y称为元素x的像，元素x称为元素y的一个原像

举例:照镜子 镜子中也有一个你 (像和原像

·定义域:集合X称为映射f的定义域 记作Df 即Df=X

·值域:X中所有元素的像组成的集合称为映射f的值域

记作Rf或f(X) 即:

Rf = f(X) = {f(x)|x∈X}

映射三要素

·集合X 即定义域Df=X

·集合Y 即值域的范围 Rf⊂Y （Y不是值域，Y包含Rf）

·对应法则f 使对每个x∈X 有唯一确定的y=f(x)与之对应

注意

·对每个x∈X 元素x的像y是唯一的

·对每个y∈Rf 元素y的原像不一定是唯一的

·映射f的值域Rf是Y的一个字集 即Rf⊂Y 不一定Rf=Y

·满射 Rf=Y

·单射 任意x1 x2 ∈X x1≠x2 有f(x1)≠f(x2)

·一一映射:满射+单射

三角函数映射法则

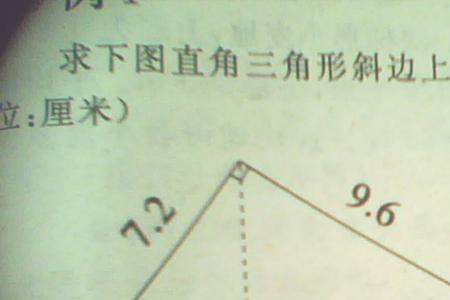
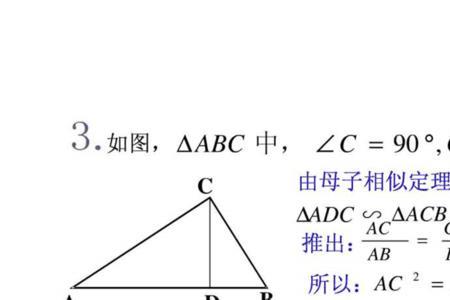
射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。