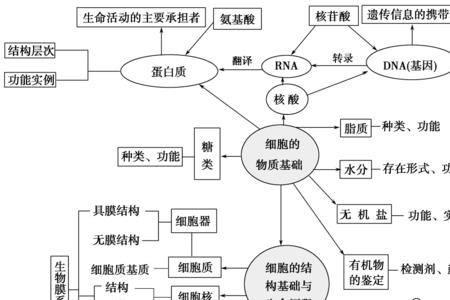
马尔科夫分析法,又称为马尔科夫转移矩阵法,是指在马尔科夫过程的假设前提下,通过分析随机变量的现时变化情况来预测这些变量未来变化情况的一种预测方法。马尔科夫是俄国数学家,他在20世纪初发现:一个系统的某些因素在转移中,第n次结果只受第n-1次结果的影响,即只与当前所处状态有关,与以前状态无关。比如:研究一个商店的累计销售额,如果现在时刻的累计销售额已知,则未来某一时刻的累计销售额与现在时刻以前的任一时刻的累计销售额都无关。
在马尔科夫分析中,引入状态转移这个概念。所谓状态是指客观事物可能出现或存在的状态状态转移是指客观事物由一种状态转移到另一种状态的概率。
如果系统未来的状况仅取决于其现在的状况,那么就可以使用马尔科夫分析。马尔科夫分析法是一种定量分析技术,可以是不连续的(利用状态间变化的概率)或者连续的(利用各状态的变化率)。
(一)适用范围
适用于对复杂系统中不确定性事件及其状态改变的定量分析。
(二)主要优点和局限性
1、主要优点:
能够计算出具有维修能力和多重降级状态的系统的概率。
2、局限性:
(1)无论是故障还是维修,都假设状态变化的概率是固定的
(2)所有事项在统计上具有独立性,因此未来的状态独立于一切过去的状态,除非两个状态紧密相接
(3)需要了解状态变化的各种概率
(4)有关矩阵运算的知识比较复杂,非专业人士很难看懂。