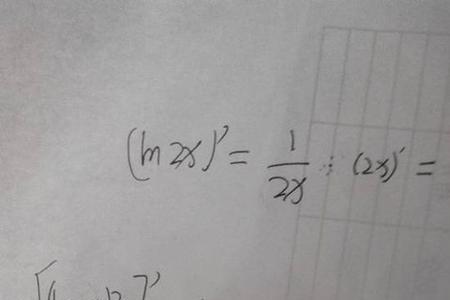x的n次方推导

用高中学的知识，是对x²、x³求导，找出规律来的，但是不能验证成立，严格推导的话需要用到的知识高中还接触不到的，我写出来你看看好了.

y=x^n

取对数：lny = n·lnx

两边同时取微分：dlny = n·dlnx

变形：(1/x)dy = n(1/x)dx

dy/dx = ny/x

将y=x^n代入上式，dy/dx = n(x^n)/x = nx^(n-1)

x的n次方推导

把x^n写成e^(nlnx)，再对e^(nlnx)求导 [e^(nlnx)]'=e^(nlnx)*(nlnx)'=x^n*(n/x)=nx^(n-1)怎么来的?(e^u)'=u'*e^u就是复合函数求导咯~