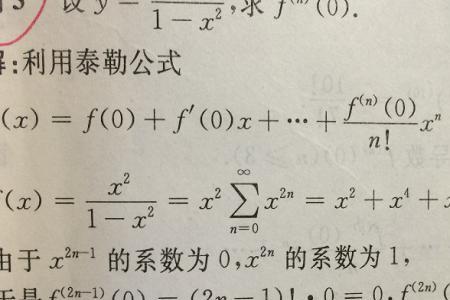n的x次方的导数

n的x次方的导数：

y=x^n

取对数：lny = n·lnx

两边同时取微分：dlny = n·dlnx

变形：(1/x)dy = n(1/x)dx

dy/dx = ny/x

将y=x^n代入上式，dy/dx = n(x^n)/x = nx^(n-1)。

导数（Derivative）是微积分中的重要基础概念。当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程，导数的四则运算法则来源于极限的四则运算法则。

n的x次方的导数

这是个指数函数的求导问题。在指数函数中，底数n＞0，且不等于1。根据指数函数的求导公式：n的x方的导数＝n的x次方•Ⅰnn。这里的符号Ⅰn是表示自然对数。自然对数是以e为底（e是无穷数列（1＋1／n）的n次方当n→∝时的极限。e＝2.718……）的对数，底e省略不写。