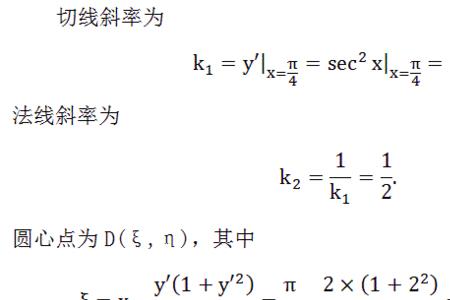若第一个圆的圆心(a,b)半径是r,第二个圆心(m,n)半径为R。设直线KX一y十C=0,由于圆与直线相切,则圆心到直线距离等于半经。所以方程组|ka-b|=r√k^2+1,丨Km-n丨=R√K^2+1。联立解出k与b,若求出k与b有4组则两圆外离。即可根据切线条数判定两圆位置关系
怎么求两个圆的公切线的方程
一、外公切线公式的求法:
设大圆半径为R,小圆半径为r,圆心距为d
过小圆圆心作垂直于大圆的半径(此半径与外公切线垂直)
则有l^2=d^2-(R-r)^2
故l=根号d^2-(R-r)^2
(l是公切线长)
二、内公切线公式的求法:
设大圆半径为R,小圆半径为r,圆心距为d
平移内公切线使公切线的一端端点与小圆圆心重合
则有l^2=d^2-(R+r)^2
故l=根号d^2-(R+r)^2