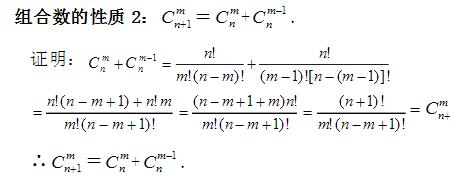二项式定理第n项的系数怎么求

方法

1

二项式展开式每一项Term包括三个部分：二项式系数，a的幂，b的幂，Term由三个部分的乘积构成。下面公式的右侧是二项式展开式。

2

下面的第一个公式是第k+1项的内容，其中系数是个组合数C，表示从n个数中选取k个的含义。第二个公式是组合数的计算方法。第三个公式是组合数中的阶层n!的计算方法。按照这三个公式就能确定k+1项的系数。

3

其次，确定第k+1项的a的次数和b的次数

第k+1项表示从n个数的名额中选择k个b，那么剩余的n-k个名额用来选择a

4

再次，二项式各项求和得到展开式

将每一项的计算结果进行求和，总共n+1项，就会得到二项式的展开式的结果

5

一个计算的例子(a+b)^4

本例子n = 4二项式展开一共有5项，下面是每一项的计算结果以及组合成展开式的结果。

6

最后，更直观的二项式系数计算的方式

每一个处于三角形内部的数字都是由它肩膀上面的两个数字求和计算得到的，三角形每一行的数字对应的二项式展开式的各项系数。可以看到刚刚的例子(a+b)^4的系数分别是1，4，6，4，1，正好对应系数三角形中第5行的数字。

总结：

1/1

1、二项式展开式每一项Term包括三个部分：二项式系数，a的幂，b的幂，Term由三个部分的乘积构成。

2、每一个处于三角形内部的数字都是由它肩膀上面的两个数字求和计算得的。

3、二项式(a+b)^n计算的核心任务是确认某一项如何表示以及如何计算。

二项式定理第n项的系数怎么求

(a+b)^n

=Cn0a^n+Cn1a^n-1b

+……

+Cnra^n-rb^r

+……

+Cnn-1ab^n-1+Cnnb^n

第n项是Cnn-1ab^n-1，具体系数要结合a，b的值

例如(2+x)^n第n项是Cnn-12x^n-1

系数是Cnn-1*2=2n