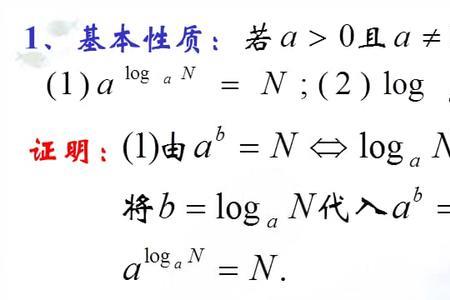lnM+lnN=ln(MN)
lnM-lnN=ln(M/N)。
理由:两个大于0且不等于1的实数M与N的积的对数,等于M的同底的对数加上N的同底的对数,即
loga(MN)=loga(M)+loga(N)。
两个大于0且不等于1的实数M除以N的商的对数,等于M的同底的对数减去N的同底的对数,即
loga(M/N)=loga(M)-loga(N)。
任何对数运算都适合上述法则。本题是自然对数,其运算当然适合上述法则。
两个ln相加减怎么计算
In=loge(e为下标,是电子的意思也就是个常数) In只是log的特例 In(M*N)=InM+InN In(M/N)=InM-InN InM^a=aInM