关于y轴对称的直线解析式

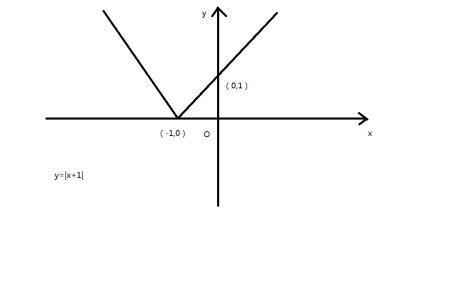
关于y轴对称的解析式为y=a(-x)²+b(-x)+c=ax²-bx+c。

二次函数（quadratic function）的基本表示形式为y=ax²+bx+c（a≠0）。二次函数最高次必须为二次， 二次函数的图像是一条对称轴

扩展资料：

一次项系数b和二次项系数a共同决定对称轴的位置。

1、当a与b同号时（即ab>0），对称轴在y轴左

2、当a与b异号时（即ab<0），对称轴在y轴右。

抛物线与x轴交点个数

1、Δ= b²-4ac>0时，抛物线与x轴有2个交点。

2、Δ= b²-4ac=0时，抛物线与x轴有1个交点。

3、Δ= b²-4ac<0时，抛物线与x轴没有交点。与y轴平行或重合于y轴的抛物线。

关于y轴对称的直线解析式

关于y轴对称两点关系是(x，y)(-x，y)

因此直线y=kx+b关于y轴对称的直线解析式就是

y=-kx+b