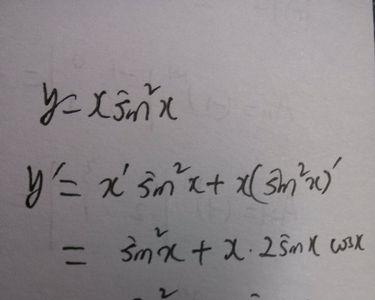y=u²,u=sinx,y=2sinxcosx=sin2x。这是一个复合函数,由正弦函数和二次函数组成。
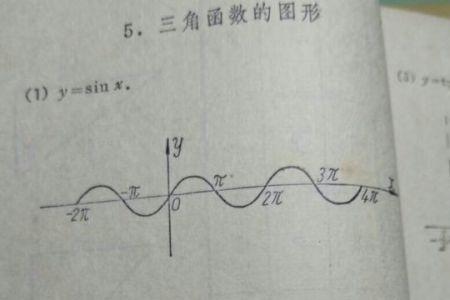
正弦(sine),数学术语,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
函数
被称为幂指函数,在经济活动中会大量涉及此类函数,注意到它很特别。既不是指数函数又不是幂函数,它的幂底和指数上都有自变量x,所以不能用初等函数的微分法处理了。这里介绍一个专门解决此类函数的方法,对数求导法。
扩展资料
导数公式
1、C'=0(C为常数)
2、(Xn)'=nX(n-1) (n∈R)
3、(sinX)'=cosX
4、(cosX)'=-sinX
5、(aX)'=aXIna
(ln为自然对数)
6、(logaX)'=(1/X)logae=1/(Xlna)
(a>0,且a≠1)
7、(tanX)'=1/(cosX)2=(secX)2
8、(cotX)'=-1/(sinX)2=-(cscX)2
9、(secX)'=tanX
secX
10、(cscX)'=-cotX
cscX。以上只提供参考
sin²的导数是
sinx的平方的导数等于sin2x。理解起来有两种方法,第一种可以看做两个sinx相乘,即sinx•sinx,然后求导就是cosxsinx+sinxcosx=2sinxcosx=sin2x
第二种方法是看做复合函数求导(麻烦),也就是2sinx•(sinx)'=2sinxcosx=sin2x。两种理解方式都可以。